Entendendo o Gráfico Boxplot e sua aplicação

Neste post, abordaremos o Gráfico Boxplot, uma ferramenta essencial na estatística para a visualização de distribuições de dados e identificação de valores atípicos (outliers). Discutiremos a estrutura e interpretação de um Boxplot, destacando seus componentes principais, como mediana, quartis e outliers. Além disso, forneceremos um exemplo prático aplicando o boxplot no contexto educacional, comparando um conjunto de notas em 3 disciplinas diferentes (Matemática, Ciência e História). Este artigo é destinado a estatísticos, analistas de dados e profissionais de áreas correlatas que buscam aprimorar suas competências em análise gráfica de dados.

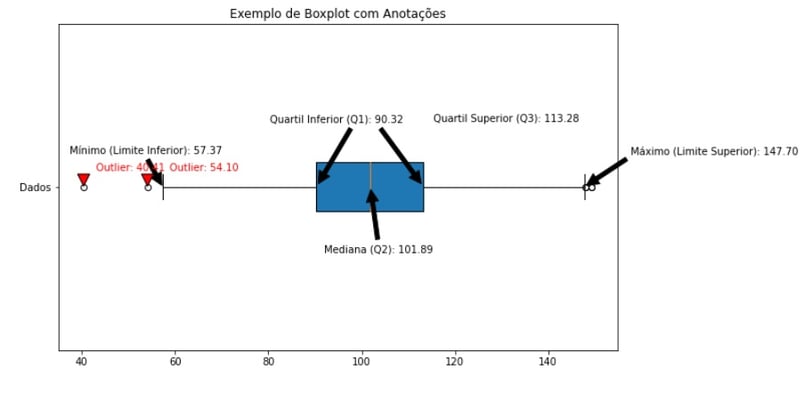
Estrutura do Boxplot

O boxplot é composto por vários elementos gráficos que juntos fornecem uma visão abrangente da distribuição dos dados, destacando os quartis, os valores atípicos (outliers) e a mediana.

Sua estrutura tem o formato de uma "caixa" que representa o intervalo interquartil (IQR) e "bigodes (whiskers)" que indicam a extensão dos dados dentro de 1,5 vezes o IQR a partir dos quartis. Os pontos fora dos bigodes são considerados outliers. Bigodes são linhas que conectam os extremos da caixa, que se estendem até os valores mínimos e máximos, excluindo outliers.

A mediana é representada por uma linha dentro da caixa, que por sua vez é delimitada pelos quartis inferior e superior. Estes quartis dividem os dados em quatro partes iguais, permitindo uma análise detalhada da variação e da dispersão dos dados.

Como Interpretar um Boxplot?

1. Mediana (Linha Central - Q2): Representa o ponto médio ou valor central dos dados, é uma medida de tendência central, que significa que 50% dos dados são menores ou iguais a esse valor.

2. Quartil Inferior (Q1) e Quartil Superior (Q3): Delimitam a caixa e representam, respectivamente, os 25% e 75% dos dados são menores que ou iguais a esses valores.

3. Limite Inferior (Mínimo): menor valor.

4. Limite Superior (Máximo): maior valor.

5. Bigodes: Indicam a faixa de dados dentro de 1,5 vezes o IQR além dos quartis.

6. Outliers: Dados que estão além dos bigodes.

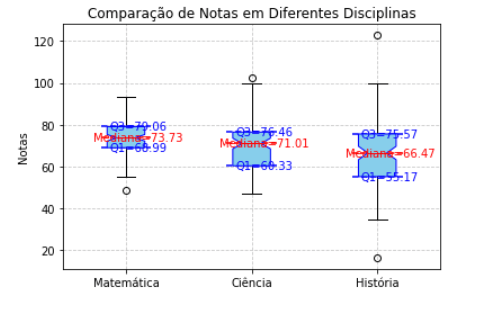
Exemplo prático

Suponhamos que três disciplinas: Matemática, Ciência e História, com um conjunto de notas de alunos entre 0 a 100 valores. Cada disciplina terá uma lista de notas de alunos, que usaremos para criar boxplots comparativos.

Análise desse Boxplot

No gráfico resultante:

1. Caixa (Área Azul): Representa o intervalo interquartil (IQR), mostrando a dispersão central das notas:

   • Q1 (Primeiro Quartil): Representa o ponto onde 25% dos dados estão abaixo, são menores que ou iguais a esse valor.

   • Mediana (Linha Vermelha - Q2 ou Segundo Quartil): Representa a mediana das notas em cada disciplina, ou seja, 50% dos dados são menores ou iguais a esse valor.

   • Q3 (Terceiro Quartil): Representa o ponto onde 75% dos dados estão abaixo, são menores que ou iguais a esse valor.

2. Bigodes: Indicam o intervalo de notas que não são consideradas outliers (geralmente 1,5 vezes o IQR a partir dos quartis).

3. Outliers (pontos fora dos bigodes): Representam notas que estão significativamente distantes da maioria dos dados.

Esse exemplo prático ajuda a visualizar como as notas dos alunos variam entre diferentes disciplinas, identificando diferenças na centralidade (mediana) e dispersão (IQR) das notas, além de destacar a presença de possíveis outliers. Observe que os valores superiores a 100 são considerados outliers, ou seja, são valores que na parte de limpeza e tratamento dos dados na análise de dados podem ser desconsiderados ou ajustados com a mediana, já que foram valores que não fazem parte do intervalo inicialmente fornecido [0,100].

Vantagens do Uso do Boxplot

Uma das principais vantagens do boxplot é a sua capacidade de resumir grandes conjuntos de dados em um formato visualmente intuitivo. Isso facilita a comparação entre diferentes conjuntos de dados, permitindo a identificação rápida de tendências, dispersões e outliers. Além disso, o boxplot é uma ferramenta robusta que não é significativamente afetada por outliers, ao contrário de outras medidas estatísticas como a média. Isso torna o boxplot uma escolha ideal para análises preliminares de dados, ou seja, análise exploratórias de dados.

Aplicações do Boxplot na Análise de Dados

O boxplot é amplamente utilizado em diversas áreas, incluindo finanças, saúde, ciências sociais e engenharia. Em finanças, por exemplo, ele pode ser usado para analisar a distribuição de retornos sobre investimentos, identificando períodos de alta volatilidade. Na área da saúde, o boxplot pode ajudar a visualizar a distribuição de características biométricas em diferentes grupos de pacientes. Em pesquisas sociais, ele pode ser útil para comparar a distribuição de respostas em diferentes amostras populacionais.

Além disso, o boxplot é frequentemente utilizado em conjunto com outras técnicas estatísticas para proporcionar uma análise mais abrangente dos dados. Ele pode ser combinado com histogramas, gráficos de dispersão (scatter plots) e outras visualizações para fornecer uma visão mais completa e detalhada dos dados sob estudo.

Conclusão

Ao compreender e aplicar o Boxplot, você poderá identificar rapidamente a variabilidade dos dados e detectar anomalias, facilitando a tomada de decisões mais certeiras por parte de pesquisadores e analistas de dados que buscam obter insights significativos com base em evidências visuais robustas.